Trie implementation in Javascript

A trie, or prefix tree, is a multi-way tree structure useful for storing strings over an alphabet. It is very efficient and handy and can be used for various purposes like auto-complete, spell-check, dictionary search, etc.

The basic idea of a Trie goes as below:

• We have a root node which represents an empty string.
• Every other node either represents a word or a prefix of one or more words.
• Each node can have atmost as many children as the size of the alphabet.

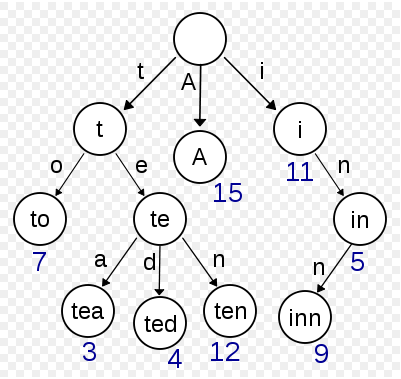
The above diagram shows a trie which stores the words “A”, “to”, “tea”, “ted”, “ten”, “i”, “in”, and “inn”.

Below is my implementation of Trie in javascript:

At each node of Trie, I store the word-count, prefix-count and the link to children.

Trie = function() {
    this.words = 0;
    this.prefixes = 0;
    this.children = [];
};

To insert a word, I recursively traverse through the trie nodes if they already exist, else I create new nodes. While traversing the nodes, I keep on storing the information in the nodes as I encounter each character in the given string.

insert: function(str, pos) {
    if(str.length == 0) { //blank string cannot be inserted
        return;
    }
    var T = this,
        k,
        child;
    if(pos === undefined) {
        pos = 0;
    }
    if(pos === str.length) {
        T.words ++;
        return;
    }
    T.prefixes ++;
    k = str[pos];
    if(T.children[k] === undefined) { //if node for this char doesn't exist, create one
        T.children[k] = new Trie();
    }
    child = T.children[k];
    child.insert(str, pos + 1);
}

Removing a word follows the similar idea as insertion.

To update, I simply remove the existing word and insert the new word.

Searching a word is trivial as we just need to check if the word count at the terminating node of the input string is greater than zero or not.

find: function(str) {
    if(str.length == 0) {
        return false;
    }
    if(this.countWord(str) > 0) {
        return true;
    } else {
        return false;
    }
}

You can get the full source code in my GitHub repository

Meanwhile you can see the auto-complete demo using my trie implementation

Links:

• Trie on Wikipedia
• Tries by Lloyd Allison
• TopCoder tutorial on Tries
• AutoComplete demo using Trie